Las cubiertas formadas por paraboloides hiperbólicos se encuentran dentro de las llamadas estructuras laminares, este tipo de estructuras se viene estudiando y construyendo de manera regular desde la primera mitad del siglo XX, para su desarrollo fue necesaria la investigación desde distintas disciplinas: la geometría, el cálculo, los materiales y la construcción.
Tomado de Superficies regladas
.
Desde que Carl Friedrich Gauss dedujera las ecuaciones de las superficies regladas, se podría decir que ningún arquitecto había sido consciente de las posibilidades que estas formas brindaban hasta Antoni Gaudí, que libre de prejuicios formales percibió las ventajas con las que cuentan en materia de construcción.
Fuente imágenes: Nieves Díaz (Deviant Art)
.
Estas formas, cuyas definiciones y ecuaciones pueden resultar complejas, se encuentran en la Naturaleza de manera más habitual de lo que se puede pensar, de lo que se puede deducir que son eficientes y rentables. Además, según Gaudí, la Naturaleza crea formas que son útiles y hermosas al mismo tiempo, por lo que, quizá, deberían ser más utilizadas que otras más comunes en arquitectura, como la esfera o el cubo.
Las estructuras laminares son elementos que cubren espacios en los
que predominan las dimensiones de la planta frente al espesor de la
lámina. Su forma y continuidad estructural es lo que las hace funcionar,
para ello tienen que ser lo suficientemente delgadas para no
desarrollar importantes tensiones de flexión, corte o torsión. Toda su
labor se basa en que todos los esfuerzos internos sean normales, de tracción o compresión, y tangenciales.
La carga debe
estar, preferiblemente, uniformemente distribuida y no presentar
variaciones bruscas ni cargas puntuales. Esto indica que el apoyo de linternas o elementos puntuales sobre
estas cubiertas complica su
resolución, y así lo demuestran los ejemplos construidos que evitan
cualquier elemento ajeno a la continuidad de la lámina.
La
forma es la característica fundamental que la hace resistir, debe
variar sus radios de curvatura sobre la superficie de manera continua,
el espesor se ha de relacionar de manera directa con el radio de
curvatura.
Las condiciones de borde tienen que ser
tales que estén libres de flexiones como el resto de la superficie. Las
generatrices del contorno pueden estar libres o unidas, esto solo hará
variar la ley de reparto de esfuerzos.
Las estructuras laminares de manera general se clasifican en tres grandes grupos:
i) el grupo de las superficies sin curvatura en el que se encuentran las láminas plegadas. En estas predomina el estado de flexión frente al de membrana.
ii) las superficies de curvatura simple, son las que tienen forma cilíndrica o cónica, en estas superficies también conviven los dos estados, pero en este caso el de membrana predomina sobre la flexión.
iii) las superficies de doble curvatura, dentro de las que se encuentra el paraboloide hiperbólico y son las que están en estado de membrana puro. Las superficies de doble curvatura pueden ser de curvatura de Gauss positiva o sinclásticas, a este grupo pertenecen los casquetes o los paraboloides elípticos. O de curvatura de Gauss negativa o anticlásticas, en el que se encuentran el paraboloide hiperbólico y el hiperboloide.
La principal diferencia entre las superficies de curvatura simple y de doble curvatura está en que las primeras
son figuras desarrollables, con curvatura de Gauss nula, y se pueden realizar a partir de figuras
planas, lo que facilita una primera aproximación al diseño y posterior
construcción.
El paraboloide hiperbólico presenta una gran ventaja frente a las
formas desarrollables y a las otras formas de doble curvatura, que se
genera a partir de una familia de rectas que se va apoyando sobre otras dos
rectas, lo que significa que es una superficie con dos
sistemas de generatrices y directrices rectilíneas que facilitan su adaptación
a plantas de carácter ortogonal típicas de la arquitectura moderna y
favorecen su construcción en cuanto a la elaboración de los encofrados y la colocación de las armaduras. Que tenga curvaturas con el
signo cambiado, y curvatura de Gauss negativa, es otra
cualidad que también la mejora frente a otras, ya que pasa a
considerarse como estructura tensada que puede ser utilizada en
estructuras textiles.
Cripta iglesia Colonia Güell (Gaudí)
El ingeniero Eduardo Torroja Miret (1899–1961) y el arquitecto Félix Candela Outeriño (1910–1997) son dos de las figuras más destacadas dentro del mundo de las láminas de hormigón armado en el siglo XX.
Si bien Antoni Gaudí, para la construcción de paraboloides hiperbólicos, contaba solo con hiladas de ladrillo o piedra sobre muros no paralelos en el espacio, Torroja y Candela ya tienen más medios a su alcance y consiguieron aprovechar al máximo las virtudes del hormigón armado.
Mercado de Abastos de Algeciras (Eduardo Torroja)
.En 1933 Eduardo Torroja, a partir de modelos a escala, se lanzó a construir la cubierta del Mercado de Abastos de Algeciras, que salvó 47,80 metros de luz con un espesor de 9 cm.
Félix Candela, años más tarde, también inició su carrera en el mundo de las láminas a través de modelos a escala. El primero fue una lámina funicular que levantó en la Escuela Experimental de Ciudad Victoria en 1950 y fue, en 1953, en la Colonia Vallejo cuando realizó el primer modelo de cubierta, a partir de trozos de paraboloide hiperbólico (hypar).
EL PARABOLOIDE HIPERBÓLICO (HYPAR)
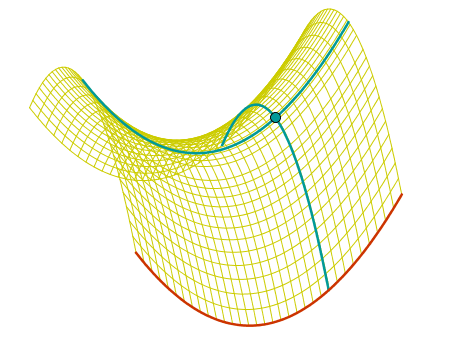
El paraboloide hiperbólico es una lámina de curvatura doble, anticlástica. Se puede definir desde dos puntos de vista diferentes: (i) a partir de dos curvas o (ii) de dos familias de rectas.
i) La superficie se genera trasladando una parábola paralela a sí misma sobre otra de curvatura inversa, si las parábolas se encuentran en dos planos que forman 90º el paraboloide hiperbólico se denomina equilátero, si no se denomina no equilátero.
ii) Expresado desde el punto de vista de una superficie reglada se define el paraboloide hiperbólico a través de dos familias de rectas, una familia - las asíntotas de las hipérbolas, generatrices- que se desplaza de manera paralela, apoyándose sobre otra formada por dos rectas - directrices- que se cruzan, de inclinaciones diferentes y separadas una determinada distancia.
Fuente: Láminas anticlásticas

.
Las secciones rectas que se dan en un paraboloide hiperbólico pueden ser parábolas si son verticales, hipérbolas si son horizontales o rectas si siguen la dirección de las generatrices. Esta aptitud para ser segmentado, llevó a Félix Candela a reflexionar sobre la posibilidad de combinar diferentes trozos, para que trabajaran de manera conjunta, siendo más eficaces que la superficie continua de un mismo hypar. Surgiendo lo que llamó "el paraguas" que admite diversas formas, en voladizo con un apoyo central o apoyado en las cuatro esquinas.Son muchos los proyectos de Félix Candela que surgen de las diferentes combinaciones de porciones de hypar:
.
– En abanico: retorciendo casi 90º los paraboloides hiperbólicos, exagerando la altura, en planta triangular y uniendo varios. Como en la iglesia de la Medalla de la Milagrosa, o la entrada a los laboratorios Lederle.
.
– Con bordes rectos: va desde la estructura formada por una sola hoja de forma cuadrada, hasta la combinación de varias hojas de formas romboidales. La inclinación respecto del eje vertical es otra de las variables que se pueden introducir, para conseguir otros efectos, como en la iglesia de San José Obrero (1959).
.
– Con bordes curvos: constituye la típica forma de silla de montar donde se perciben las parábolas más fácilmente. En 1951 se construye la cubierta del Pabellón de Rayos Cósmicos, que se considera el primer cascarón de Candela con esta forma.
Capilla de Cuernavaca (Félix Candela)
.
En la cubierta de la Capilla de Cuernavaca (1958, Morelos, México) Candela enseñó las dos posibilidades de borde curvo, la parábola en el espacio principal y la hipérbola en el contacto con el suelo. – Bóvedas por arista: en este caso se utiliza el hypar no equilátero, ya que en el equilátero al tener las direcciones rectas perpendiculares entre sí, coincidirían con las aristas de una bóveda cuadrada y, por tanto, serían rectas. Esto dificulta demasiado el cálculo, ya que hay que considerar un sistema de coordenadas oblicuas.
La primera bóveda de este tipo se levantó en 1955 en el edificio de la Bolsa de Valores de México y en ella Félix Candela intuye la posibilidad del borde libre (de esfuerzos), ya que cada punto del borde curvo está conectado a las aristas por dos líneas rectas, a través de las que se pueden derivar las cargas, para llevarlas a los apoyos, dejando así el borde libre de esfuerzos tangenciales o normales.
Destilería de Bacardí en Cuautitlán (Félix Candela)
.En todo cálculo estructural uno de los objetivos primordiales es la obtención de un diseño óptimo. Tradicionalmente, en el campo de las estructuras, un diseño óptimo es aquel que reduce al mínimo su propio peso, por lo que este ha sido el fin de los grandes calculistas, pero no siempre es el factor determinante, o se prioriza sobre otras cualidades, como el costo o la forma.
Toda cubierta requiere una superficie continua que proteja a los usuarios de los agentes climatológicos. El hormigón armado es uno de los pocos materiales que lo consigue, simplemente ayudado por láminas impermeabilizantes. Además, es un material que puede responder, en cada punto, al esfuerzo que se requiere de manera exacta, con ambas cualidades se consigue reducir materiales de cobertura y desperdiciar material que no está trabajando.
Las únicas desventajas han sido, en tiempos pasados, la dificultad de controlar la calidad y la homogeneidad del hormigón dentro del mismo elemento o la misma obra.
Las membranas son estructuras que minimizan la cantidad de material, ya que se evitan los esfuerzos de flexión y cortante, con lo que el hormigón solo tiene que trabajar a compresión y, ayudado por el acero, a tracción.
Para que una superficie funcione como cáscara necesita formas curvas, cosa que dificulta su diseño, tanto a nivel gráfico como constructivo. La forma que tiene el paraboloide hiperbólico presenta las mejores cualidades como membrana a nivel estructural.
a) Su doble curvatura hace que tenga la cualidad de estructura tensada por lo que cada línea de carga funciona a compresión, cuando tiene su concavidad al interior; y a tracción cuando tiene la convexidad hacia el interior. Es decir, hace simultáneamente la función arco y cable. Además dota de la suficiente rigidez a la superficie, no siendo necesarias estructuras secundarias del tipo arcos fajones.
b) El modo de generarse a partir de dos familias de rectas permite poder definirla a partir de coordenadas cartesianas, por medio de sencillas ecuaciones de primer grado, lo que facilita la distribución de las armaduras necesarias, creando los nervios sobre las rectas generatrices.
c) Los bordes generados por las secciones de planos rectos permiten obtener rectas, parábolas o hipérbolas, que la hace muy apta para enlazar bordes rectos con formas curvas o viceversa. Con esto, a partir de trozos de hypar se pueden generar infinitas formas. Además si los bordes se alejan de la dirección de una de las directrices, reparten mejor los esfuerzos y se consigue liberar el borde, dando aspecto de liviandad a la estructura.

Los problemas fundamentales son a nivel de ejecución, ya que es fácil la fisuración por retracción. Las condiciones acústicas que presenta, también pueden suponer un inconveniente, ya que son peores que en las formas de curvatura simple, cilindros y conos.
La desventaja fundamental del paraboloide hiperbólico y su caída en desuso, como de otras formas de membrana, aparte de corrientes o estilos arquitectónicos, se debe a la elaboración del encofrado. A partir de los años setenta, el incremento del costo de la mano de obra hacía difícil la construcción de este tipo de cubiertas, pese a que los encofrados son fáciles de montar, por medio de tablas rectas, una contra otra, siguiendo las direcciones de las generatrices, pero son laboriosos de realizar, además de no ser reutilizables. La prefabricación, tanto de las cubiertas como de los encofrados, no ha sido posible llevarla a cabo hasta ahora.
Estas cubiertas, para que funcionen, deben ser continuas y no se ha logrado una unión artificial que permita la continuidad de los esfuerzos. Se pueden obtener superficies similares, pero su modo de trabajar no sería el mismo y, por lo tanto, los espesores en relación a las luces que cubren, no serían tan buenos como en las estructuras laminares.
La solución pasa por encontrar un material que no requiera el uso de encofrados. Se ha intentado la utilización de materiales ligeros que permitan el modelado, como algunos metales, pero su resistencia no se puede comparar a la del hormigón. La otra opción es la de conseguir unos encofrados prefabricados y reutilizables, como hace el arquitecto suizo Heinz Isler, es un buen modo de que estas cubiertas sean factibles, pero lógicamente se pierde la gran variedad de posibilidades que el paraboloide hiperbólico proporciona.
Información extraída de: "Cubiertas formadas por paraboloides hiperbólicos: Ventajas en su funcionamiento estructural y en su construcción" (autora: Mónica Morales Segura, Actas VI Congreso Nacional de Historia de la Construcción, 2009 )
_________________________________________________________
La arquitectura no construida de Félix Candela (proyectos 1939-1997)





















La implementacion en la Arquitectura es sorprendente
ResponderEliminarMuy buen documento
ResponderEliminarEncontré algunos pocos errores conceptuales en este trabajo.
ResponderEliminarMuy bien.
ResponderEliminar