Un poliedro o sólido arquimediano tiene las siguientes características:
- El segmento determinado por dos vértices cualesquiera es siempre interior al cuerpo (es un poliedro convexo).
- Todos sus vértices son puntos de una esfera.
- Sus caras son polígonos regulares de, al menos, dos tipos diferentes.
- Todas sus aristas tienen la misma longitud.
- Los ángulos poliedros determinados por las aristas que convergen en cada vértice son convexos (es un polígono convexo). Es decir, la suma de los ángulos internos de todas las caras con un vértice común es menor que 360°.
- Sus caras pertenecen a dos o a lo sumo a tres de las siguientes categorías de polígonos regulares: triángulos equiláteros, cuadrados, pentágonos, hexágonos, octógonos y decágonos.
- Los ángulos poliedros determinados por las aristas que convergen en cada vértice son congruentes, es decir, pueden superponerse exactamente por traslaciones, rotaciones o/y reflexiones.
- Satisface (por ser un poliedro convexo) la relación de Euler: Vértices + Caras = Aristas + 2
GEOMETRÍA de los 13 Poliedros ARQUIMEDIANOS
Tetraedro truncado (truncated tetrahedron)
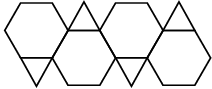
8 Caras (4 hexágonos + 4 triángulos)
12 Vertices
18 Aristas
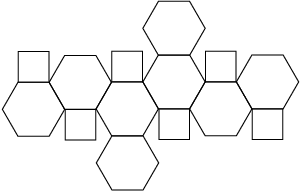
14 Caras (6 cuadrados + 8 hexágonos)
24 Vértices
36 Aristas
24 Vértices
36 Aristas
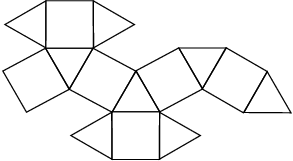
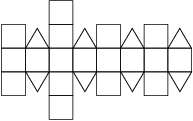
26 Caras (18 cuadrados + 8 triángulos)
24 Vértices
48 Aristas
24 Vértices
48 Aristas
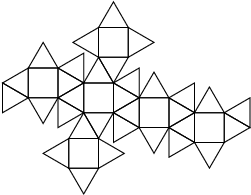
38 Caras (6 cuadrados + 32 triángulos)
24 Vértices
60 Aristas
24 Vértices
60 Aristas
Icosidodecaedro (icosidodecahedron)
32 Caras (12 pentágonos + 20 triángulos)
30 Vértices
60 Aristas
30 Vértices
60 Aristas
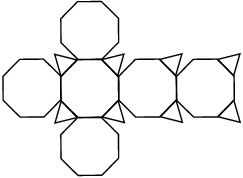
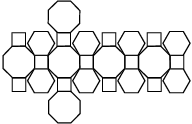
26 Caras (6 octógonos + 8 hexágonos + 12 cuadrados )
48 Vértices
72 Aristas
48 Vértices
72 Aristas
Dodecaedro truncado ( truncated dodecahedron)
32 Caras (12 decágonos + 20 triángulos )
60 Vértices
90 Aristas
32 Caras (12 decágonos + 20 triángulos )
60 Vértices
90 Aristas
32 Caras (12 pentágonos + 20 hexágonos )
60 Vértices
90 Aristas
60 Vértices
90 Aristas
62 Caras (12 pentágonos + 30 cuadrados + 20 triángulos )
60 Vértices
120 Aristas
60 Vértices
120 Aristas
Gran rombicosidodecaedro o Icosidodecaedro truncado (great rhombicosidodecahedron)
62 Caras (12 decágonos + 20 hexágonos + 30 cuadrados )
120 Vértices
180 Aristas
62 Caras (12 decágonos + 20 hexágonos + 30 cuadrados )
120 Vértices
180 Aristas
____________________
Enlaces relacionados:
POLIEDROS ARQUIMEDIANOS
http://mathworld.wolfram.com/ArchimedeanSolid.html
http://cyt-ar.com.ar/cyt-ar/index.php/Poliedros_arquimedeanos
Poliedros Ciencia y Tecnología
http://mathworld.wolfram.com/ArchimedeanSolid.html
http://cyt-ar.com.ar/cyt-ar/index.php/Poliedros_arquimedeanos
Poliedros Ciencia y Tecnología














me encanta,la mejor profe
ResponderEliminarun beso alex