Los métodos infinitesimales de Leibniz (1646-1716) ejercerían una profunda influencia en los matemáticos europeos continentales. En particular, su discípulo suizo Jakob Bernoulli (1654-1705) publicaría en mayo de 1690 un trabajo en la revista Acta Eruditorum donde establece la propiedad tautócrona de la cicloide haciendo uso del cálculo diferencial e integral. La curva cicloide se define como el lugar geométrico de un punto fijo
de una circunferencia que gira sin deslizamiento a lo largo de una
recta. Siendo \( \theta \) el desplazamiento angular de una
circunferencia de radio R, se obtienen las ecuaciones paramétricas:
En junio de 1696, Johann Bernoulli, hermano de Jakob, se había trasladado a Groningen (Holanda) para ocupar
la cátedra de matemáticas de aquella universidad, y propone en Acta Eruditorum el problema de la braquistócrona:
"determinar la curva, entre las infinitas posibles, por la que un cuerpo desciende en el menor tiempo posible entre dos puntos que no están ni en posición vertical ni horizontal, movido únicamente por efecto de la gravedad".
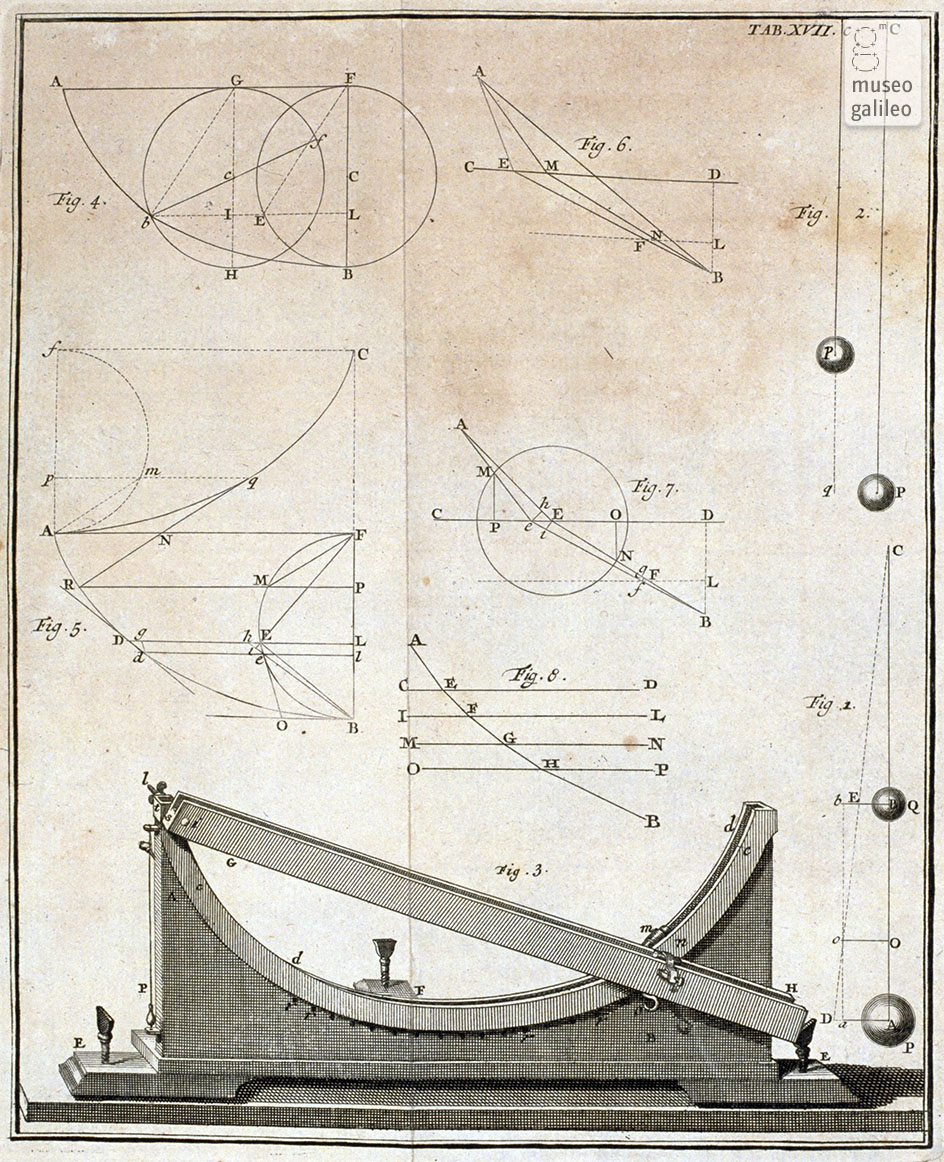
Braquistócrona (círculo) / Galileo Galilei
El problema de la curva de tiempo más breve (braquistócrona) ya había sido considerado
cerca de setenta años antes por Galileo Galilei, quien, sin poseer la potente
herramienta del cálculo infinitesimal de Leibniz , había propuesto (erróneamente) que dicha curva
debía de ser un arco de circunferencia.
El reto lanzado por
Johann, iba dirigido a los más brillantes matemáticos del mundo. El
propio Johann había añadido el inquietante dato de que dicha curva era bien conocida entre los matemáticos. El plazo para la recepción de soluciones fue establecido hasta finales de 1696, aunque Johann aseguraba que "media hora de profunda reflexión sería más que suficiente para una mente capaz". En total se recibieron cuatro propuestas de solución de Leibniz, el marqués de L´Hôpital, y los dos hermanos
Jakob y Johann Bernoulli. Todas las soluciones propuestas, a excepción
de la de L'Hôpital, establecían que la curva braquistócrona era una
curva cicloide.
El método de resolución propuesto por Jakob Bernoulli era mucho más general que la solución propuesta por su
hermano Johann, y ejerció una profunda influencia en Leonhard Euler, quien, junto a Lagrange, instauraría las bases del Cálculo de Variaciones.
Newton publicó de manera anónima su solución al reto de Bernoulli en Philosophical Transactions, una brillante y escueta propuesta que concluía que la curva braquistócrona era la cicloide.

Johann Bernoulli (1667-1748)
Johann tomará en consideración un problema de óptica aparentemente sin relación con el problema de la braquistócrona. Conocía el Principio del menor tiempo de Fermat: "la luz va de un punto A a un punto B siguiendo la trayectoria que requiere el menor tiempo". Este principio se aplica para encontrar la trayectoria de un rayo de luz en un medio de densidad variable, donde, en general, la luz se desplazará en curvas en lugar de líneas rectas, debido a la variación de la velocidad.
Suponiendo un medio óptico estratificado, en cada capa la velocidad de la luz es constante, y la velocidad varía de capa a capa. En el caso de que la velocidad del rayo de luz que desciende aumentara, se refractará cada vez más alejado de la vertical. Aplicando la ley de Snell:
\( \dfrac{\sin \alpha _{1}}{v_{1}}= \dfrac{\sin \alpha _{2}}{v_{2}}= \dfrac{\sin \alpha _{3}}{v_{3}} = ...\)
Si se considera que las capas son cada vez más delgadas y numerosas, entonces, en el límite, la velocidad de la luz, conforme desciende el rayo verificará:
\( \dfrac{\sin \alpha }{v}=constante \)
Johann supone que un cuerpo que desciende de A a B, puede escoger la trayectoria como lo hace un rayo de luz, empleando el menor tiempo posible. Además, por el Principio de conservación de la energía, la velocidad alcanzada en un nivel dado queda determinada por su pérdida de energía potencial que se transforma en energía cinética \( \frac{m v^{2}}{2} = mgy\) , es decir, la velocidad es proporcional a la raíz cuadrada de la distancia desde donde cae: \( v=\sqrt{2gy} = k· \sqrt{y} \); por tanto \( sin \alpha=K· \sqrt{y} \)
\( y=f(x) \) ; \(\tan \beta = \frac{dy}{dx} \) ; \( \alpha + \beta=90º \)
\( sin\alpha = cos\beta = \dfrac{1}{sec\beta }=\dfrac{1}{\sqrt{1+tan^{2}\beta }} =\dfrac{1}{\sqrt{1+\left ( \dfrac{dy}{dx} \right )^{2}}} = K· \sqrt{y} \)
Obtenemos: \( y \left [ 1+\left ( \frac{dy}{dx} \right )^2 \right ] = C \) ecuación diferencial de la braquistócrona, según Johann Bernoulli.
\( dx= \left ( \dfrac{y}{C-y} \right )^\frac{1}{2}dy \)
Efectuamos el cambio de variable \( \tan\phi = \left ( \frac{y}{C-y} \right )^\frac{1}{2} \) ;
\(dx=\tan\phi ·dy \)
\( y= (C-y) \tan^2\phi \)
\( y· (1+\tan^2\phi) = C · \tan^2\phi \)
\( y= C \cdot\sin^2\phi \)
\( dy= 2C · \sin\phi ·\cos\phi · d\phi\)
\(dx=\tan\phi ·dy=2C· \sin^2\phi ·d\phi = C(1-\cos 2\phi) d\phi \)
Integrando:
\( x= \frac{C}{2}\left ( 2\phi-\sin2\phi \right )+C_{1} \)
imponiendo las condiciones iniciales \( (x,y)= (0,0) ; \phi=0 \) obtenemos \(C_{1}=0 \)
Por tanto \( x= \frac{C}{2}\left ( 2\phi-\sin2\phi \right )\)
Además \( y= C · \sin^2\phi= \frac{C}{2}\left ( 1-\cos2\phi \right ) \)
Si efectuamos el cambio \( \frac{C}{2} =R \) ; \( 2\phi= \theta \) obtenemos las ecuaciones paramétricas de la cicloide:
\( x= R (\theta-\sin \theta) \)
\( y= R (1-\cos \theta) \)
(Tomado de Ecuaciones Diferenciales, George F. Simmons)
______________________________
Orígenes del Cálculo Diferencial e Integral (I)
Orígenes del Cálculo Diferencial e Integral (II)
Acta Eruditorum: Leibniz's Papers on Calculus























