Georg Cantor y la Teoría de los Infinitos

La idea del infinito era motivo de horror entre los matemáticos griegos de la época clásica. Pero lentamente penetraba en la mente matemática el concepto del infinito. Galileo Galilei sintió la necesidad de introducirlo en la matemática. En 1636 Galileo en su obra "Dialogo sopra i due massimi sistemi del mondo" enunció  la idea de que había conjuntos infinitos.

El desarrollo de la matemática tendía en esa misma dirección, sin llegar a un concepto claro sobre el infinito actual, siendo aceptado el infinito potencial (los números primos pueden ser infinitos). En el siglo XIX, surgieron descubrimientos matemáticos que indicaban que los números racionales e irracionales no tenían el mismo peso en el conjunto de los números reales.

Cauchy y Weierstrass habían conseguido establecer los fundamentos del Cálculo sobre la noción de límite, pero los matemáticos estaban empezando a ver que algunas de las cuestiones fundamentales del Cálculo descansaban sobre las propiedades de los conjuntos de números racionales y reales.

 Georg Cantor y su esposa, Vally Guttmann

Georg Cantor había nacido en San Petersburgo (1845) en el seno de una familia muy religiosa, padre protestante y madre católica. Cantor desarrollará toda su vida un gran interés por los temas teológicos, en particular por los relacionados con la naturaleza de lo infinito. Cuando tiene 12 años su familia se traslada a Alemania. Sobresale en matemáticas y en 1867 completa su doctorado en la Universidad de Berlín, donde estudia con Weierstrass, que le pone en contacto con el desarrollo riguroso del Cálculo. La investigación de Cantor sobre los puntos débiles del Análisis Matemático le lleva a considerar las diferencias intrínsecas entre conjuntos de números y la importancia de encontrar un modo de comparar los tamaños de los mismos.

"Dos conjuntos M y N, son equivalentes (equipotentes) si es posible ponerlos, mediante una cierta ley, en relación mutua tal que a cada elemento de uno ellos le corresponde uno y solo un elemento del otro." (Georg Cantor)

De manera brillante Cantor comparaba conjuntos, no necesariamente finitos. Se embarcó en una tarea que le llevaría por caminos extraños, y serían muchos los matemáticos que ridiculizarían sus esfuerzos, entre ellos Cauchy.

Los primeros trabajos de Cantor se refirieron a la teoría de números y fueron publicados entre 1867 y 1871.

Un suceso de gran importancia marcó su futuro como matemático. En 1872 realizó un viaje a Suiza. Allí conoció a Richard Dedekind con quien estableció una relación de profunda amistad hasta el final de su vida. Muchas cartas se intercambiaron desde entonces y, aún cuando en ellas no se incluían muchos temas de matemática, el pensamiento abstracto y lógico de Dedekind influyó profundamente en Cantor.

Cantor comienza probando que el conjunto de los números naturales  \( \mathbb{N}= \left \{ 1,2,3,4,... \right \}      \) y el de los números pares \(  \mathbb{P}= \left \{ 2,4,6,8,... \right \} \) tienen la misma cardinalidad, es decir, son equipotentes, existe una correspondencia biunívoca entre ambos:
\[  1\leftrightarrow 2; 2\leftrightarrow 4; 3\leftrightarrow 6; 4\leftrightarrow 8;...    \]

Por tanto existe la misma cantidad de números naturales que de números pares.

Cantor estudió el conjunto de los números enteros, \( \mathbb{Z}\), y concluyó que era equivalente su cardinal infinito y el de los números naturales. Establece el siguiente orden en  \( \mathbb{Z}= \left \{ 0,1,-1,2,-2,3,-3,4,-4,... \right \}\), es decir,
\[  1\leftrightarrow 0; 2\leftrightarrow 1; 3\leftrightarrow -1; 4\leftrightarrow 2; 5\leftrightarrow -2; 6\leftrightarrow 3...    \]
Y por tanto la correspondencia biunívoca viene dada por:
 \[  \frac{1+(-1)^{n}\cdot (2n-1)}{4}    \]

Cantor observa que puede establecer relaciones entre conjuntos infinitos y el conjunto \(\mathbb{N}\), y determina que dichos conjuntos son numerables. Y va más allá, introduce una nueva categoría de número "transfinito", que representa el número de elementos de un conjunto numerable, que Cantor inicialmente denomina A (en alusión a abzaehlbar, que significa contable en alemán), actualmente denominado  Aleph cero.

Por tanto cardinal \(\mathbb{N}\) = cardinal \(\mathbb{P}\) = cardinal \(\mathbb{Z}\)= Aleph cero

Cantor se plantea si \(\mathbb{Q}\), el conjunto de los números racionales será también numerable. Todo parecía indicar que no lo sería, los números racionales están densamente distribuidos, a diferencia de los números enteros; entre dos números racionales hay infinitos racionales. Así que cualquiera conjeturaría que su cardinal es de una categoría superior a la de \(\mathbb{N}\), pero Cantor probó que también era numerable!!

La demostración era sencilla, estableció un orden en las fracciones, organizadas tal y como se observa en la siguiente tabla:

Dada una fracción cualquiera, por ejemplo \(  \frac{4}{5} \), podemos localizarla en la fila 5ª y la columna (teniendo en cuenta los positivos y negativos anteriores a 4) será la 7ª (doble de 3 más 1), en el caso de las fracciones negativas, \(  -\frac{4}{5} \), se encontrará en la fila 5ª y la columna 8ª (doble de 4). Así queda comprobado que la tabla contiene todas las fracciones, con redundancia, pues contiene todas las fracciones equivalentes a una dada. Cuando efectuamos el recuento se hará en el orden propuesto por Cantor, siguiendo las flechas y omitiendo en el recuento las equivalentes a las ya contadas. Hay tantos números racionales como naturales.

El conjunto de los números racionales, \(\mathbb{Q}\), es numerable y por consiguiente igual al conjunto de los números naturales. Cardinal \(\mathbb{Q}\) = Aleph cero.

Parecía que todos los conjuntos infinitos representaban el mismo número transfinito, Aleph cero, pero Cantor observó que no era así. 

La escuela pitagórica  ya reconocía la existencia de números inconmensurables, y Euclides demostró que \(  \sqrt{2}  \) era un número irracional.

En 1874 el mundo matemático aprendió otra lección del trabajo de Cantor, existía un conjunto no numerable, precísamente eran los números irracionales,  \(\mathbb{I}\), que tantos quebraderos de cabeza habían dado a los matemáticos griegos.

Cantor publica en 1874 "Ueber eine Eigenschaft des inbegriffs aller reellen algebraischen Zahlen" iniciando un camino revolucionario. En principio, el conjunto no numerable encontrado por Cantor era el conjunto de los números reales. Demostraba que ningún intervalo de números reales por pequeño que fuera podía ser equivalente a los números naturales.

En 1891 vuelve a tratar esta cuestión y da una sencillísima demostración de la no numerabilidad de cualquier intervalo de números reales. Cantor demuestra que \( (0,1)\subset \mathbb{R} \) no es numerable. La demostración, por reducción al absurdo, supone que todos los números del intervalo pueden ser ordenados:
\( 0,a_{1} a_{2} a_{3} a_{4}... \);  \( 0,b_{1} b_{2} b_{3} b_{4}..  \); \(   0,c_{1} c_{2} c_{3} c_{4}... \);  \( 0,d_{1} d_{2} d_{3} d_{4}... \) ...

Y Cantor describe un nuevo número que no formaría parte de esa colección: \( 0,a_{0} b_{0} c_{0} d_{0}... \) de manera que \( a_{0}\neq a_{1}; b_{0}\neq b_{2}; c_{0}\neq c_{3}; d_{0}\neq d_{4};...   \) y \(  a_{0}, b_{0}, c_{0}, d_{0},...  \) no tomen ni el valor 0 ni 9 (con lo que evita aproximaciones que conviertan al nuevo número en alguno de la lista, por ejemplo \( 0,499999999...= \frac{1}{2} \) ). De esta sencilla manera Cantor obtiene un nuevo número real que no está en la lista, pese a que suponíamos que estaban todos.

Para extender este razonamiento a cualquier intervalo \( (a,b) \) basta establecer la relación biunívoca mediante \( y= a + (b-a)\cdot x  \)  lo que garantiza la misma numerabilidad que el intervalo \( (0,1) \). Y para extender el razonamiento a todos los números reales basta considerar la correspondencia biunívoca entre \( x\in (0,1) \) e \( y \in \mathbb{R} \):
\[  y= \frac{2x-1}{x-x^{2}}    \]
Y por tanto concluye que el cardinal de los números reales, \( \mathbb{R}= \mathbb{Q} \cup  \mathbb{I} \), describe un nuevo número transfinito mucho mayor que Aleph cero, que denomina \(c \) (cardinal del continuo), también conocido como Aleph uno.

Además demuestra que la unión de conjuntos numerables es numerable, lo que le lleva a concluir que son los números irracionales, \(\mathbb{I}\), los que no son numerables, ya que los números racionales sí lo son. Cardinal \(\mathbb{I}\) = \( c\) o Aleph uno.

Así que un conjunto numerable (de cardinal infinito), \(\mathbb{Q}\),  resulta ser una cantidad insignificante pese a su comprobada densidad. Cantor afirma que los números racionales son muy escasos cuando se amplia la escena a los números reales, donde dominan los números irracionales. El trabajo de Cantor arrojaba luz sobre las diferencias intrínsecas entre subconjuntos de números reales, que explicaría algunos fenómenos inquietantes al desarrollar los fundamentos del Cálculo y el Análisis de funciones.

Tras demostrar la no numerabilidad de los números irracionales, Cantor va más allá, y concluye que serán los números reales trascendentes (no algebraicos) los que provocan esa no numerabilidad.

En el momento en el que Cantor está desarrollando su teoría del infinito se creía que existía una gran cantidad de números algebraicos, es decir aquellos que  pueden obtenerse como solución de una ecuación polinómica cuyos coeficientes son números racionales. Y, por el contrario, se creía que los números trascendentes (no algebraicos) era escasos y difíciles de obtener.

Constante de Liouville 

Euler fue el primero que especuló sobre la existencia de estos números. El primer ejemplo de número trascendente fue, L, dado por Joseph Liouville en 1844. En el año 1873 Charles Hermite demuestra que el número \( e \) es trascendente (ver demostración). En 1882 Lindemann prueba que \( \pi  \) además de irracional es trascendente.

Cantor acomete una nueva genialidad, demuestra que ¡¡los números algebraicos eran numerables!! Veamos su razonamiento.

Considera \(  a_{0}x^{n}+a_{1}x^{n-1}+a_{2}x^{n-2}+...+a_{n-2}x^{2}+a_{n-1}x+a_{n}=0  \) ecuaciones algebraicas con coeficientes naturales. El Teorema Fundamental del Álgebra afirma que dicha ecuación tendrá al menos una raíz real o compleja, si n es impar sabemos que tendrá necesariamente, al menos, una solución real. El conjunto de todas las soluciones de todas las ecuaciones algebraicas serán los números algebraicos.

Cantor introduce el concepto de altura, H, de una ecuación algebraica. H es la suma de los valores absolutos de los coeficientes de la ecuación más el grado menos 1. Así la altura de \( 3 x^{2}+ 5x -7 \)  será    \( H=3+5+7+2-1=16 \). Cantor demuestra que existe una cantidad finita de ecuaciones que tienen la misma altura H. Así que las agrupa según el valor H, empezando por H=1, forma subgrupos teniendo en cuenta el grado, dentro de esta agrupación considera el orden de nuevo teniendo en cuenta el coeficiente principal, de mayor a menor, si coincidieran considera el orden respecto del valor del segundo coeficiente, etc, De esta manera las ecuaciones se pueden ordenar de manera unívoca, lo que equivale a decir que las ecuaciones son numerables.

 

Raíces de la ecuación cúbica

Cada ecuación algebraica puede tener una o varias raíces reales, pero ninguna ecuación puede tener más raíces que su grado y por consiguiente que su altura H. De manera que las raíces, como las ecuaciones, se pueden ordenar. Cantor observa que si cada número algebraico que se obtiene de esta manera se suprime al presentarse por segunda vez, se evitan las repeticiones y cada número algebraico tendrá un lugar definido en esa lista ordenada, es decir, los números algebraicos al igual que las ecuaciones algebraicas son numerables.

Así que teniendo en cuenta que el conjunto de los números reales no es numerable y que los números algebraicos sí lo son, son los números trascendentes los que generan la no numerabilidad.

Esto resultó provocador e inquietante en la época de Cantor. Sólo se conocían unos pocos números no algebraicos (trascendentes) y allí estaba Cantor sosteniendo convencido que los números trascendentes existían en gran cantidad y todo ello sin mostrar ni un solo ejemplo de número trascendente.

Éste fue el legado de la singular publicación de Cantor en 1874. Fueron muchos los que admiraron sus resultados, pero los más conservadores tomaron con reserva las locas demostraciones de Cantor, al que tildaban de místico. Cantor creía apasionadamente en sus hallazgos, y aún nos depararía más sorpresas con sus descubrimientos.

Cantor sorprendió de nuevo afirmando y demostrando de una manera increiblemente sencilla que "los puntos de un segmento cualquiera de una recta no es una cantidad menor que la cantidad de puntos de la recta infinita", es decir un segmento AB y una recta r ¡¡contienen la misma cantidad de puntos!!

La correspondencia biunívoca entre los puntos del segmento AB y la recta r se obtiene simplemente trazando una imaginaria línea desde los puntos auxiliares D y C, que cortará al segmento y a la recta en dos únicos puntos. Lo que demuestra que por cada punto del segmento obtenemos otro que le corresponde sobre la recta, es decir, existe el mismo número de puntos en el segmento que en la recta infinita.

Cantor empezaba a cuestionarse si sería posible encontrar un cardinal transfinito superior a \( c  \) y creyó que la solución estaría en considerar un cuadrado de dos dimensiones, (0,1)  x  (0,1).

Escribe a Dedekind en 1874 con esta cuestión, y el propio Cantor cree que no es posible establecer una correspondencia biunívoca entre ese cuadrado y el intervalo \( (0,1) \). Cree que claramente el cuadrado tiene una mayor abundancia de puntos. Hasta que en 1877 descubre que dicha correspondencia ¡¡sí existe!!

Demostró que pese a ser de dimensión 2, ambos conjuntos tenían cardinalidad \( c  \). Inmediatamente escribió a Dedekind mostrándole su asombro: "lo veo pero no lo creo".

Considera S, el cuadrado \( (0,1) X (0,1)\), siendo \((x,y)  \) coordenadas  donde \( 0<x< 1 ; 0<y< 1 \)
Sea \((x,y)  \) punto de S  tal que \( x= 0,a_{1} a_{2} a_{3} a_{4}... \)   \( y= 0,b_{1} b_{2} b_{3} b_{4}..  \) le hace corresponder \( r =  0,a_{1}b_{1}a_{2}b_{2}a_{3} b_{3}... \) que pertenece al intervalo \( (0,1) \).

Y dado \( r  \) del intervalo se puede obtener el punto \((x,y)  \) de S, siguiendo el procedimiento inverso.

Existe alguna singularidad, algún \( r  \) puede no tener su correspondiente en S, por ejemplo: \(0,10909090...\) daría lugar a \( (0,1999999...; 0,000000.. )\) y sabemos que la segunda coordenada no puede ser nula.

No supuso ningún problema pues lo que Cantor obtuvo es que el cardinal de S es menor que \( c  \) y como obviamente \( c  \) es menor que el cardinal de S, la igualdad de ambos cardinales está asegurada (teorema de Cantor-Schröder-Bernstein).

Cantor pudo demostrar fácilmente que incluso todos los puntos del plano tienen la misma cardinalidad que el intervalo  \( (0,1) \), ya que en el plano entendido como el producto cartesiano \( X x Y \) , puede asimilarse cada eje (recta) en correspondencia con el intervalo  \( (0,1) \), lo que nos lleva al cuadrado S.

Incluso un cubo tridimensional no aumenta la cardinalidad, sigue siendo \( c  \) o Aleph uno. El procedimiento es el mismo que el que utilizó para el cuadrado S.

Cantor va aún más allá; dice y comprueba que hasta para un espacio que tenga una infinidad numerable de dimensiones, el cardinal transfinito de dicho espacio será  \( c  \). Parecía que \( c  \) sería el último cardinal transfinito. Pero no sería el final.

 

 Hipótesis del continuo

En la primavera de 1884, mientras trabajaba febrilmente en la hipótesis del continuo, con 40 años de edad, Cantor sufrió por primera vez una de las crisis que habrían de repetirse con diversa intensidad durante el resto de su larga vida, llevándolo al ingreso en el Hospital Neuropático de Halle.

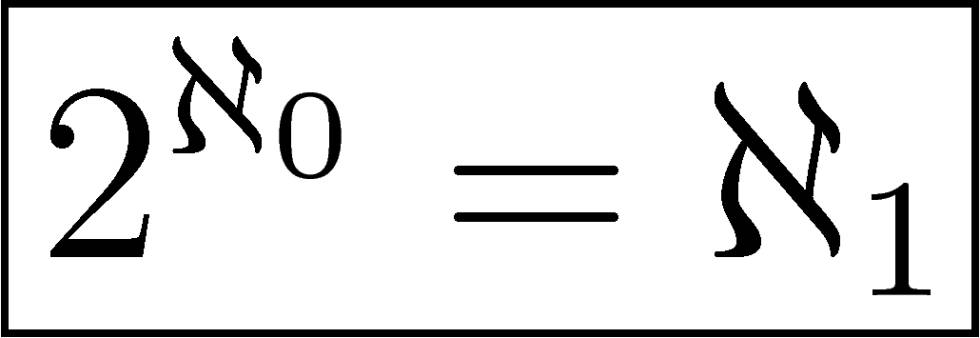
Llegó a dudar de la solidez de su obra. Muchos de sus mejores estudios sobre la teoría del infinito fueron realizados entre crisis. Al recuperarse de ellas, notaba que su mente se tornaba extraordinariamente clara.

En 1891 Cantor logró demostrar que existían cardinales transfinitos mayores y además en cantidades increibles. Se conoce como Teorema de Cantor, en él garantiza que existe una cadena interminable de números transfinitos, cada vez mayores.

Cantor llevó las matemáticas hasta un territorio inexplorado en el que se empezaban a fundir con los sueños de la filosofía y la metafísica. Cantor encontró significado religioso a su teoría de los transfinitos:

 "No albergo dudas respecto a la verdad de los transfinitos que he reconocido con la ayuda de Dios". 

Su actitud mística le favoreció poco frente a sus críticos. Uno de ellos era Leopold Kronecker, toda una institución en la Universidad de Berlín.

Georg Cantor

En 1899 sufre un golpe terrible con la muerte de su hijo Rudolf, volvió a ser hospitalizado en 1902, 1904, 1907 y 1911. Tras el alta solía quedarse largos períodos en casa sentado, inmóvil y callado. Fue una vida triste. La muerte le sobrevino el 6 de enero de 1918, durante un ingreso en el Hospital Neuropático de Halle.

David Hilbert declaró: "Nadie nos expulsará del paraíso que Cantor ha creado".

 Monumento dedicado a Georg Cantor (Halle, Google Maps)

____________________________________
Viaje a través de los genios (William Dunham)

Cantor, el conquistador del infinito

Números trascendentes: desarrollo histórico 

 Los números transfinitos

Controversias sobre los Fundamentos de la Matemática