Dibujo realizado por Bézier
Las llamadas "curvas de Bézier" deben su nombre a Pierre Etienne Bézier (1910-1999), ingeniero de Renault de 1933 a 1975. Como responsable del departamento "méthodes mécaniques" a principios de la década de los sesenta empieza a preocuparse por la utilización de herramientas informáticas en el diseño de carrocerías. Las herramientas de CAD (Computer Aided Manufacturing) basadas en polígonos no representaban bien las superfícies curvas. Bézier logró un método fácil de usar y a la vez exacto para describir curvas a partir de cuatro puntos. El sistema se lanzó en 1968 y en 1975 ya estaba en pleno uso. Las "curvas de Bézier" han sido un elemento clave para el posterior desarrollo de la informática gráfica vectorial, tanto 3D como 2D.
Antes que Bézier dos matemáticos que trabajaban para Boeing y Citroën (James Ferguson y Paul de Casteljau) llegaron a los mismos resultados. Pero sus hallazgos no fueron conocidos hasta mucho más tarde porque se guardaron bajo secreto industrial.
Las curvas de Bézier son segmentos de línea conectados entre sí por nodos. Cada segmento lo entendemos como un vector con un punto inicial y un punto final que definen la línea. A estos se añaden "dos puntos de control" que definen la curvatura de la misma. Los puntos de control parten de las tangentes de cada uno de los puntos extremos o nodos. Cuando los cuatro puntos están alineados tenemos una recta. Cuando los puntos de control se separan tenemos algún tipo de línea curva. Esta curva está siempre contenida dentro de un polígono cuadrilátero cuyos vértices son dichos cuatro puntos. La curva se calcula a partir de una interpolación creada por una secuencia de funciones que se basa en las coordenadas de los puntos. Esto hace que sea escalable y se vea bien a cualquier nivel de ampliación.
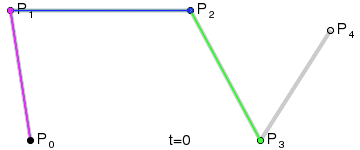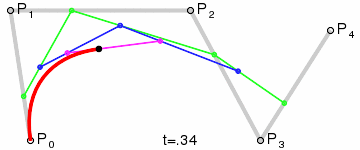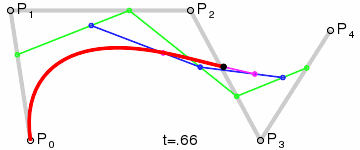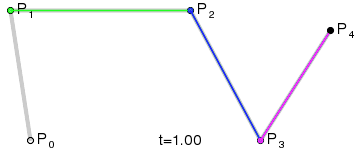
Las curvas de Bézier son segmentos de línea conectados entre sí por nodos. Cada segmento lo entendemos como un vector con un punto inicial y un punto final que definen la línea. A estos se añaden "dos puntos de control" que definen la curvatura de la misma. Los puntos de control parten de las tangentes de cada uno de los puntos extremos o nodos. Cuando los cuatro puntos están alineados tenemos una recta. Cuando los puntos de control se separan tenemos algún tipo de línea curva. Esta curva está siempre contenida dentro de un polígono cuadrilátero cuyos vértices son dichos cuatro puntos. La curva se calcula a partir de una interpolación creada por una secuencia de funciones que se basa en las coordenadas de los puntos. Esto hace que sea escalable y se vea bien a cualquier nivel de ampliación.

________________
_______________
Fuente A Primer on Bézier Curves _______________

No hay comentarios:
Publicar un comentario